Diferența dintre transformările Laplace și Fourier

Laplace vs. Fourier se transformă
 

Atât transformarea Laplace, cât și transformarea Fourier sunt transformări integrale, care sunt utilizate cel mai frecvent ca metode matematice de rezolvare a sistemelor fizice modelate matematic. Procesul este simplu. Un model matematic complex este convertit într-un model mai simplu, de rezolvat, utilizând o transformare integrală. Odată ce modelul mai simplu este rezolvat, se aplică transformarea integrală inversă, care ar oferi soluția modelului original.

De exemplu, deoarece majoritatea sistemelor fizice au ca rezultat ecuații diferențiale, ele pot fi transformate în ecuații algebrice sau în ecuații diferențiale ușor de rezolvat cu ajutorul unei transformări integrale. Rezolvarea problemei va deveni mai ușoară.

Care este transformarea lui Laplace?

Având o funcție f (T) unei variabile reale T, transformarea lui Laplace este definită de integrale 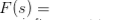(ori de câte ori există), care este o funcție a unei variabile complexe s. Acesta este de obicei marcat cu L f (T). Transformarea inversă Laplace a unei funcții F(s) este considerată a fi funcția f (T) în așa fel încât L f (T) = F(s), iar în nota matematică obișnuită pe care o scriem, L ^-1F(s) = f (T).Transformarea inversă poate fi făcută unică dacă funcțiile null nu sunt permise. Se poate identifica aceste două ca operatori liniari definiți în spațiul funcțional și este ușor de observat și faptul că L ^-1L f (T) = f (T), dacă funcțiile null nu sunt permise.

Următorul tabel afișează transformările Laplace ale unor funcții cele mai comune.

Care este transformarea Fourier??

Având o funcție f (T) unei variabile reale T, transformarea lui Laplace este definită de integrale 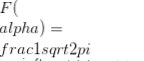(ori de câte ori există) și este de obicei marcată de F f (T). Transformarea inversă F ^-1F(α) este dată de integrale . Transformarea Fourier este, de asemenea, liniară și poate fi considerată ca un operator definit în spațiul funcțional.

Folosind transformarea Fourier, funcția inițială poate fi scrisă după cum urmează, cu condiția ca funcția să aibă doar un număr finit de discontinuități și este absolut integrabilă.

Care este diferența dintre transformările Laplace și Fourier?

• Transformarea Fourier a unei funcții f (T) este definit ca 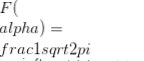, în timp ce transformarea lui laplace este definită ca fiind .
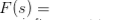• Transformarea Fourier este definită numai pentru funcțiile definite pentru toate numerele reale, în timp ce transformarea Laplace nu necesită definirea funcției pe setarea numerelor reale negative.
• Transformarea Fourier este un caz special al transformării Laplace. Se poate observa că ambele coincid pentru numere reale ne-negative. (adică luați s în Laplace să fie iα + β Unde α și β sunt reale astfel încât e ^β= ¹/_{√ (2ᴫ)})
• Fiecare funcție care are o transformare Fourier va avea o transformare Laplace, dar nu invers.