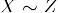Diferența dintre egal și echivalent
 Share
Share
Diferența principală - egală vs. echivalentă
Egal și echivalent sunt termeni care sunt folosiți frecvent în matematică. principala diferență între egal și echivalent este termenul egal se referă la lucruri care sunt similare în toate aspectele, întrucât termenul echivalent se referă la lucruri care sunt similare într-un anumit aspect. Rețineți că în teoria seturilor, cuvintele "egale" și "echivalente" au semnificații specifice, după cum vom vedea mai jos.
Ce înseamnă egal
În general, două lucruri sunt egale dacă sunt similare în toate privințele.
În cazul teoriei seturilor, două seturi sunt egale dacă ambele conțin aceleași elemente. Ordin în care sunt enumerate într-un set, nu contează. De exemplu, să presupunem
 și
și
 atunci,
atunci,
decorul  este egal cu setul
este egal cu setul  .
.
Ce înseamnă echivalentul mediu
Două lucruri se pot spune că sunt echivalente dacă sunt similare într-o anumită condiție. Prin urmare, dacă sunt două entități echivalent în mare măsură depinde pe baza condiției pe care o folosim pentru a descrie echivalența acestora. De exemplu, numerele 2 și 7 sunt echivalente în sensul că sunt ambele numere prime. Cu toate acestea, dacă condiția în care suntem interesați constată dacă numerele sunt egale, atunci în acest sens 2 și 7 sunt nu echivalent. Folosim simbolurile  sau
sau  pentru a indica acest lucru
pentru a indica acest lucru  și
și  sunt echivalente.
sunt echivalente.
Odată ce un criteriu a fost definit, lucrurile echivalente satisfac relații de echivalență:
- reflexivitatea:
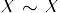
- Simetrie: Dacă
 , atunci
, atunci 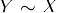
- tranzitivitate: Dacă
 și
și 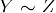 , atunci
, atunci 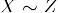
În teoria seturilor, sunt două seturi echivalent dacă au același număr de elemente. Nici elementele nu trebuie să fie aceleași, numai numărul de elemente trebuie să fie același. De exemplu, să presupunem
 și
și
 atunci,
atunci,
seturile  și
și  sunt echivalente.
sunt echivalente.

Simboluri pentru exprimarea egalității și a echivalenței
Diferența dintre egal și echivalent
Semnificația generală
Când sunt două lucruri egal, ele sunt similare în toate aspectele.
Când sunt lucrurile echivalent, ele sunt similare într-un anumit aspect.
În teoria seturilor
Când sunt două seturi egal, ele conțin aceleași elemente.
Când sunt două seturi echivalent, ele conțin același lucru Un numar de element.
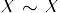
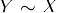
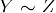 , atunci
, atunci