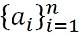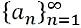Diferența dintre secvență și serie

În matematică și statistică, linia care desemnează secvența și seria este subțire și neclară, din cauza căreia mulți cred că acești termeni sunt unul și același lucru. Cu toate acestea, noțiunea de secvență diferă de serii în sensul că secvenţă se referă la un aranjament în ordinea particulară în care termenii înrudiți urmează unul altuia, adică are o primă unitate identificată, o a doua unitate, a treia unitate și așa mai departe.

Atunci când o secvență respectă o anumită regulă, se numește progresie. Nu este exact același lucru serie care este definită ca sumare a elementelor unei secvențe. Luați o citire a articolului pentru a cunoaște diferența semnificativă dintre secvență și serie.

Conținut: Seria secvențelor Vs

Diagramă de comparație

Bazele comparației	Secvenţă	Serie
Sens	Secvența este descrisă ca set de numere sau obiecte care urmează unui anumit model.	Seria se referă la suma elementelor din secvență.
Ordin	Important	Uneori important
Exemplu	1, 3, 5, 7, 9, 11 ... n ...	1 + 3 + 5 + 9 + 11 ... n ...

Definiția secvenței

În matematică, un set ordonat de obiecte sau numere, ca a₁, A₂, A₃, A₄, A₅, A₆… A_{n ... .}se spune că sunt într-o secvență, dacă, după regulă, are o anumită valoare. Membrii secvenței sunt numiți termen sau element care este egal cu orice valoare a numărului natural. Fiecare termen dintr-o secvență este legat de termenul precedent și de succes. În general, secvențele au o regulă sau un model ascuns, care vă ajută să aflați valoarea următorului termen.

Termenul n este funcția întregului n (pozitiv), considerat ca termen general al secvenței. O secvență poate fi finită sau infinită.

Secvență finită: O secvență finită este una care se oprește la sfârșitul listei de numere a₁, A₂, A₃, A₄, A₅, A₆… A_n, este reprezentat de:
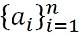
Secvență infinită: O secvență infinită se referă la o secvență care este neterminată, a₁, A₂, A₃, A₄, A₅, A₆… A_{n ... .}., este reprezentat de:

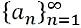
Definiția Series

Adăugarea termenilor unei secvențe (a_n), este cunoscut sub numele de serie. Ca și secvență, seriile pot fi, de asemenea, finite sau infinite, unde o serie finită este una care are un număr finit de termeni scrise ca₁+ A₂+ A₃ + A₄+ A₅ + A_{6 +}… A_n. Spre deosebire de serii infinite, unde numărul de elemente nu este finit sau care sunt nesfârșite, scrise ca a₁+ A₂+ A₃ + A₄+ A₅ + A_{6 +}… A_n+_{... .}

În cazul în care un₁+ A₂+ A₃ + A₄+ A₅ + A_{6 +}… A_n = S_n, apoi S_n este considerată ca suma pentru n elemente ale seriei. Suma termenilor este adesea reprezentată de litera greacă sigma (Σ). prin urmare,

Diferențele cheie între secvență și serie

Diferența dintre secvență și serie poate fi trasă în mod clar din următoarele motive:

Secvența este definită ca colecția de numere sau obiecte care urmează unui model definit. Atunci când elementele secvenței sunt adăugate împreună, ele sunt cunoscute ca serii.
Ordinul contează într-o secvență, deoarece există o anumită regulă care prescrie modelul secvenței. Prin urmare, 1, 2, 3, 3 este diferit de 3, 1, 2. Pe de altă parte, într-o ordine de serie a aspectului poate sau nu poate contează, ca în cazul seriei absolut convergente ordinea nu contează. Deci, 1 + 2 + 3 este la fel ca 3 + 1 + 2, doar secvența lor este diferită.

Concluzie

Progresiunea aritmetică (A.P.) și Progresia geometrică (G.P.) sunt și secvențe, nu serii. Progresiunea aritmetică este o secvență în care există o diferență comună între termenii consecutivi, cum ar fi 2, 4, 6, 8 și așa mai departe. Dimpotrivă, într-o evoluție geometrică, fiecare element al secvenței este multiplu comun al termenului precedent, cum ar fi 3, 9, 27, 81 și așa mai departe. În mod similar, secvența Fibonacci este, de asemenea, una din secvențele infinite populare, în care fiecare termen este obținut prin adăugarea celor doi termeni precedenți 1, 1, 3, 5, 8, 13, 21 și așa mai departe.

Educaţie