Cum de a calcula jumătate de viață
 Share
Share
În această secțiune vom învăța despre timpul de înjumătățire și vom determina formula pentru a calcula timpul de înjumătățire. În radioactivitate, jumătate de viață este timpul necesar pentru jumătate de nuclee radioactive într-o probă a unui izotop radioactiv pentru a se descompune. Numărul de nuclee radioactive dintr-un eșantion se diminuează exponențial în timp. Pentru a calcula timpul de înjumătățire, prin urmare, se folosește matematica decăderii exponențiale. Half-life este un concept extrem de important pentru aplicațiile de radioactivitate. Radioizotopii introduși la organe în radioterapie, de exemplu, nu trebuie să rămână prea mult timp în corpul pacientului. Pe de altă parte, izotopii folosiți pentru datarea artefactelor istorice trebuie să aibă o jumătate de viață lungă, astfel încât suficient de mulți au rămas până în prezent pentru a determina vârsta obiectelor.
Diferența dintre natura aleatorie și spontană a decăderii radioactive
Degradarea radioactivă este clasificată ca ambele întâmplător și spontan.
- Degradarea radioactivă este aleatorie deoarece nu putem determina când un nucleu dat se va deteriora sau va determina cât timp va dura înainte ca un nucleu dat să se degradeze. În consecință, fiecare nucleu radioactiv într-o probă are aceeași probabilitate de a se descompune la un moment dat.
- Degradarea radioactivă este spontană deoarece nu este afectată de condițiile externe.
Ce este Half Life
Numărul de nuclee radioactive dintr-o probă este în scădere, deoarece, odată ce nucleul se descompune prin decăderea alfa, beta și gamma, acestea nu pot suferi din nou același proces de dezintegrare. Numărul de nuclee radioactive din eșantion scade exponențial.
activitate, sau degradare,este rata de schimbare a numărului de nuclee radioactive. Acest lucru este dat de,

Semnul negativ semnifică faptul că numărul de nuclee radioactive dintr-o probă este in scadere peste orar. $ latex \ lambda & s = 1 $ este numit degradare constantă. Aceasta dă probabilitatea ca un anumit nucleu să se degradeze pe unitate de timp. Constanta de dezintegrare are o valoare specifică pentru orice proces de dezintegrare nucleară dat. Cu cât este mai mare  , cu cât probabilitatea de dezintegrare este mai mare, iar numărul de nuclee radioactive din probă se diminuează mai repede.
, cu cât probabilitatea de dezintegrare este mai mare, iar numărul de nuclee radioactive din probă se diminuează mai repede.
Dacă numărul de nuclee radioactive dintr-o probă la un moment dat  este
este  , apoi numărul de nuclee radioactive
, apoi numărul de nuclee radioactive  în eșantion după un timp
în eșantion după un timp  este dat de:
este dat de:

Numărul de nuclee radioactive din eșantion scade exponențial. Jumătate de viață ( ) Este timpul necesar pentru numărul de nuclee radioactive în timp pentru a se reduce la jumătate. Dacă desenați un grafic cu privire la modul în care numărul de nuclee radioactive din eșantion variază în timp, obținem următorul grafic:
) Este timpul necesar pentru numărul de nuclee radioactive în timp pentru a se reduce la jumătate. Dacă desenați un grafic cu privire la modul în care numărul de nuclee radioactive din eșantion variază în timp, obținem următorul grafic:

Cum se calculeaza Half Life - Curba decaderii radioactive
Cum se calculează activitatea
Activitatea eșantionului este proporțională cu numărul de nuclee radioactive prezente. Deci, putem face o declarație echivalentă,

Unde  este activitatea probei la timp
este activitatea probei la timp  , cu
, cu  activitatea atunci când
activitatea atunci când  .
.
Dacă se desenează un grafic al activității în funcție de timp, se va obține un grafic cu aceeași formă (adică, de asemenea, activitatea se descompune exponențial).
Activitatea este măsurată cu unitatea SI becquerel (Bq). O activitate de 1 Bq corespunde unei rate de 1 decădere per secundă. curie (Ci) este o altă unitate utilizată pentru măsurarea activității. 1 Ci = 3,7 x 1010 Bq.
Formula de viață de jumătate
Vom deduce acum o formulă pentru a obține timpul de înjumătățire de la constanta dezintegrării. Începem cu,

Dupa o vreme  , numărul de jumătăți de nuclee radioactive. Asa de,
, numărul de jumătăți de nuclee radioactive. Asa de,  , sau
, sau

Luând logaritmul natural al ambelor părți, obținem:

Așadar,

Cum de a calcula jumătate de viață
Exemplul 1
Indiu-112 are o durată de înjumătățire de 14,4 minute. O probă conține 1,32 × 1024 atomi de indiu-112.
a) Găsiți constanta de dezintegrare
b) Aflați câți atomi de Indiu-112 ar fi rămas în proba după 1 oră.
a) Din moment ce  ,
,

b) Utilizarea  ,
,  atomi.
atomi.
Exemplul 2
În timpul unui tratament pentru cancerul tiroidian, pacientului i se administrează o probă de iod-131 pentru ingestie, care are o activitate de 1,10 MBq. Timpul de înjumătățire al iodului 131 este de 8,02 zile. Găsiți activitatea iodului-131 în corpul pacientului după 5 zile de la ingestie.
Folosim  . În primul rând, lucrăm
. În primul rând, lucrăm  :
:

Atunci,
 MBq.
MBq.
Notă:
- Am calculat direct constanta de dezintegrare pe zi și a menținut timpul de înjumătățire și în zile. Deci zilele au fost anulate când am calculat
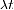 și nu a fost nevoie să se transforme ori în secunde (care ar fi funcționat, de asemenea, dar ar fi implicat un pic mai mult calcul)
și nu a fost nevoie să se transforme ori în secunde (care ar fi funcționat, de asemenea, dar ar fi implicat un pic mai mult calcul) - În realitate, activitatea ar fi mai mică. Acest lucru se datorează faptului că există și o perioadă de viață biologică asociată cu activitatea. Aceasta este rata la care pacientul excreta nucleele radioactive din corpul lor.
Exemplul 3
Se calculează timpul de înjumătățire al unui izotop radioactiv a cărui activitate se reduce cu 4% peste 1000 de ani.
4% = 0,04. Acum avem
 . Luând în ambele părți,
. Luând în ambele părți,
 pe an.
pe an.
 216 de ani.
216 de ani.
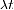 și nu a fost nevoie să se transforme ori în secunde (care ar fi funcționat, de asemenea, dar ar fi implicat un pic mai mult calcul)
și nu a fost nevoie să se transforme ori în secunde (care ar fi funcționat, de asemenea, dar ar fi implicat un pic mai mult calcul)