Diferența între media și mediană
 Share
Share
 Tendința centrală implică tendința punctelor de date de a se grupa în jurul valorii de valoare centrală sau medie. Cele două metode cele mai frecvent utilizate ale tendinței centrale sunt medii și mediane. Însemna este definită ca fiind valoarea "centrală" a setului de date dat în timp ce median este cea mai "mijlocie" valoare din setul de date dat.
Tendința centrală implică tendința punctelor de date de a se grupa în jurul valorii de valoare centrală sau medie. Cele două metode cele mai frecvent utilizate ale tendinței centrale sunt medii și mediane. Însemna este definită ca fiind valoarea "centrală" a setului de date dat în timp ce median este cea mai "mijlocie" valoare din setul de date dat.
O masura ideala a tendintei centrale este una definita clar, usor de inteles, pur si simplu calculabila. Ar trebui să se bazeze pe toate observațiile și pe cele mai puțin afectate de observațiile extreme prezente în setul de date.
Oamenii se confruntă adesea cu aceste două măsuri, dar este faptul că ele sunt diferite. Acest articol subliniază în mod specific diferențele de bază dintre medie și mediană. Uită-te.
Conținut: Medie Vs Mediană
Diagramă de comparație
| Bazele comparației | Însemna | Median |
|---|---|---|
| Sens | Mean se referă la media simplă a setului de valori sau cantități date. | Medianul este definit ca numărul de mijloc dintr-o listă de valori ordonată. |
| Ce este? | Este o medie aritmetică. | Este o medie pozițională. |
| reprezintă | Centrul de greutate al setului de date | Centrul de greutate al setului de date Punctul central al setului de date |
| aplicabilitate | Distributie normala | Distribuția înclinată |
| Aberante | Mean este sensibil la valori. | Mediana nu este sensibilă la valori extreme. |
| Calcul | Media se calculează prin adăugarea tuturor observațiilor și apoi prin împărțirea valorii obținute cu numărul de observații. | Pentru a calcula valoarea mediană, setul de date este aranjat în ordine crescătoare sau descendentă, atunci valoarea care intră în mijlocul exact al noului set de date este mediană. |
Definiția Mean
Media reprezintă măsura larg utilizată a tendinței centrale, care este definită ca medie a setului de valori. Acesta reprezintă modelul și valoarea cea mai comună a intervalului de valori dat. Se poate calcula, atât în seriile discrete, cât și în cele continue.
Media este egală cu suma tuturor observațiilor împărțită la numărul de observații din setul de date. Dacă valoarea asumată de o variabilă este egală, media acesteia va fi, de asemenea, aceeași. Media poate fi de două tipuri, media eșantionului (xj) și media populației (μ). Acesta poate fi calculat cu formula dată:
- Media aritmetică:
 unde Σ = sigma literei grecești, denumește "suma ..."
unde Σ = sigma literei grecești, denumește "suma ..."
n = număr de valori - Pentru seria discretă:
 unde, f = frecvența
unde, f = frecvența - Pentru servicii continue:
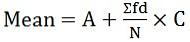 unde d = (X-A) / C
unde d = (X-A) / C
A = Medie presupusă
C = divizorul comun
Definiția Median
Mediana este o altă măsură importantă a tendinței centrale, folosită pentru a împărți valoarea în două părți egale, adică o jumătate mai mare a distribuției eșantionului, a populației sau a probabilității din jumătatea inferioară. Este cea mai mare valoare de mijloc, care se obține atunci când observațiile sunt sortate într-o ordine specifică, fie în ordine crescătoare, fie în ordine descrescătoare.
Pentru calcularea valorii mediane, mai întâi de toate, aranjați observațiile de la cel mai mic la cel mai mare sau cel mai mare până la cel mai mic, apoi aplicați formula adecvată, conform condițiilor prezentate mai jos:
- Dacă numărul de observații este ciudat:
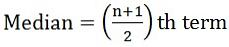 unde n = numărul de observații
unde n = numărul de observații - Dacă numărul de observații este chiar:
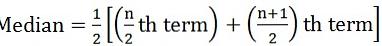
- Pentru serii continue:
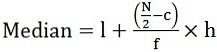 unde, l = limita inferioară a clasei mediane
unde, l = limita inferioară a clasei mediane
c = frecvența cumulativă a clasei mediane precedente
f = frecvența clasei mediane
h = lățimea clasei
Diferențele cheie între media și mediană
Diferențele semnificative dintre media și media sunt prezentate în articolul prezentat mai jos:
- În statistici, o medie este definită ca medie simplă a setului de valori sau cantități date. Se spune că valoarea mediană este numărul mediu dintr-o listă de valori ordonată.
- În timp ce media reprezintă media aritmetică, mediana este media pozițională, în esență, poziția setului de date determină valoarea mediană.
- Mediul conturează centrul de greutate al setului de date, în timp ce valoarea mediană evidențiază cea mai mare valoare a setului de date.
- Media este adecvată pentru datele distribuite în mod normal. În celălalt capăt, mediana este cea mai bună atunci când distribuția datelor este înclinată.
- Media este foarte afectată de valoarea extremă, care nu este în cazul unei mediane.
- Media se calculează prin adăugarea tuturor observațiilor și apoi prin împărțirea valorii obținute cu numărul de observații; rezultatul este mediu. Spre deosebire de mediană, setul de date este aranjat în ordine crescătoare sau descendentă, atunci valoarea care intră în mijlocul exact al noului set de date este mediană.
Exemplu
Găsiți media și mediana setului de date dat:
58, 26, 65, 34, 78, 44, 96
Soluție: Pentru a calcula media, trebuie să împărțiți suma observațiilor cu numărul de observații,

 Mean = 57,28
Mean = 57,28
Pentru a calcula mediana, mai întâi de toate, aranjați seria într-o secvență, adică cea mai mică până la cea mai înaltă,
26, 34, 44, 58, 65, 78, 96
 unde n = numărul de observații
unde n = numărul de observații
Concluzie
După examinarea punctelor de mai sus, putem spune că aceste două concepte matematice sunt diferite. Media aritmetică sau medie este considerată cea mai bună măsură a tendinței centrale, deoarece conține toate caracteristicile unei măsuri ideale, dar are un dezavantaj că fluctuațiile de prelevare influențează media.
În același mod, mediana este, de asemenea, definită fără echivoc și ușor de înțeles și calculată, iar cel mai bun lucru despre această măsură este că nu este afectat de fluctuațiile de prelevare a probelor, dar singurul dezavantaj al median este că nu se bazează pe toate observații. Pentru clasificarea la sfârșitul deschis, media este preferată în mod normal în raport cu media.
 unde Σ = sigma literei grecești, denumește "suma ..."
unde Σ = sigma literei grecești, denumește "suma ..." unde, f = frecvența
unde, f = frecvența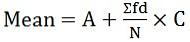 unde d = (X-A) / C
unde d = (X-A) / C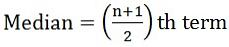 unde n = numărul de observații
unde n = numărul de observații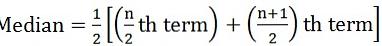
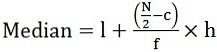 unde, l = limita inferioară a clasei mediane
unde, l = limita inferioară a clasei mediane Median = 4lea termen = 58
Median = 4lea termen = 58