Diferența dintre testul T și ANOVA
 Share
Share
 Există o linie subțire de demarcare în mijlocul t-testului și ANOVA, adică atunci când trebuie comparată populația a numai două grupuri, t-test este folosit, dar atunci când mijloace de mai mult de două grupuri trebuie să fie comparate, ANOVA este preferată.
Există o linie subțire de demarcare în mijlocul t-testului și ANOVA, adică atunci când trebuie comparată populația a numai două grupuri, t-test este folosit, dar atunci când mijloace de mai mult de două grupuri trebuie să fie comparate, ANOVA este preferată.
Testul T și analiza varianței abreviate ca ANOVA, sunt două tehnici statistice parametrice utilizate pentru a testa ipoteza. Deoarece acestea se bazează pe ipoteza comună, cum ar fi populația din care se prelevează eșantionul ar trebui distribuită în mod normal, omogenitatea varianței, eșantionarea aleatorie a datelor, independența observațiilor, măsurarea variabilei dependente la raport sau la nivelul intervalelor, Două.
Aici, este un articol prezentat pentru tine de a înțelege diferența semnificativă dintre t-test și ANOVA, aruncați o privire.
Conținut: T-test Vs ANOVA
Diagramă de comparație
| Bazele comparației | T-test | ANOVA |
|---|---|---|
| Sens | Testul T este un test de ipoteză utilizat pentru a compara mijloacele a două populații. | ANOVA este o tehnică statistică utilizată pentru a compara mijloacele a mai mult de două populații. |
| Statistici de testare | (xi-μ) / (s / √n) | Între variația eșantionului / variația eșantionului |
Definiția T-test
Testul t este descris ca un test statistic care examinează dacă mijloacele populației a două eșantioane diferă foarte mult una de alta, folosind distribuția t care este folosită atunci când abaterea standard nu este cunoscută, iar dimensiunea eșantionului este mică. Este un instrument pentru a analiza dacă cele două eșantioane sunt extrase din aceeași populație.
Testul se bazează pe t-statistică, care presupune că variabila este distribuită în mod normal (distribuție în formă de clopot simetric) și media este cunoscută, iar variația populației este calculată din eșantion.
În t-test, ipoteza nulă ia forma H0: μ (x) = μ (y) față de ipoteza alternativă H1: μ (x) ≠ μ (y), în care μ (x) și μ (y) reprezintă mijloacele populației. Gradul de libertate al testului t este n1 + n2 - 2
Definiția ANOVA
Analiza variației (ANOVA) este o metodă statistică, utilizată în mod obișnuit în toate acele situații în care trebuie făcută o comparație între mai mult de două resurse ale populației, cum ar fi randamentul culturii din soiuri multiple de semințe. Este un instrument vital de analiză pentru cercetător care îi permite să efectueze testul simultan. Atunci când folosim ANOVA, se presupune că eșantionul este extras din populația distribuită în mod normal, iar varianța populației este egală.
În ANOVA, valoarea totală a variației într-un set de date este împărțită în două tipuri, adică suma alocată pentru șansă și suma alocată anumitor cauze. Principiul său de bază este de a testa diferențele dintre mijloacele populației, evaluând variația variației în cadrul grupului, proporțională cu variația variației între grupuri. În cadrul eșantionului, varianța se datorează tulburărilor aleatorii inexplicabile, în timp ce tratamentul diferit poate provoca varianța de eșantionare.
Cu ajutorul acestei tehnici, testăm ipoteza nulă (H0) în care toate mijloacele populației sunt aceleași sau ipoteze alternative (H1) în care cel puțin o medie a populației este diferită.
Diferențe cheie între testul T și ANOVA
Diferențele semnificative dintre testul T și ANOVA sunt discutate în detaliu în următoarele puncte:
- Un test de ipoteză care este folosit pentru a compara mijloacele a două populații se numește t-test. O tehnică statistică care se utilizează pentru a compara mijloacele a mai mult de două populații este cunoscută sub numele de Analiza variației sau ANOVA.
- Statisticile de testare pentru testul T sunt:
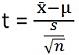 Statisticile de testare pentru ANOVA sunt:
Statisticile de testare pentru ANOVA sunt: 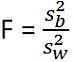
Concluzie
După examinarea punctelor de mai sus, se poate spune că t-test este un tip special de ANOVA care poate fi folosit atunci când avem doar două populații pentru a le compara. Deși șansele de erori ar putea crește dacă t-testul este utilizat atunci când trebuie să comparăm mai mult de două mijloace ale populațiilor în mod concurent, de aceea se folosește ANOVA
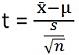 Statisticile de testare pentru ANOVA sunt:
Statisticile de testare pentru ANOVA sunt: