Cum să găsiți asimptotele unui hyperbola
 Share
Share
Hiperbolă
Hiperbola este o secțiune conică. Termenul hiperbolă se referă la cele două curbe deconectate prezentate în figură.
Dacă axele principale coincid cu axele carteziene, ecuația generală a hiperbola este de forma:

Aceste hiperbola sunt simetrice în jurul axei y și sunt cunoscute sub numele de hyperbola axei y. Hiperbola simetric în jurul axei x (sau hyperbola în axa x) este dat de ecuație,
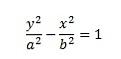 Cum să găsiți asimptotele unui hiperbolă
Cum să găsiți asimptotele unui hiperbolă
Pentru a găsi asimptotele unei hiperbola, utilizați o simplă manipulare a ecuației parabolei.
i. Mai întâi aduceți ecuația parabolului la forma de mai sus
Dacă parabola este dată ca mx2+ny2=L, prin definirea
A= √ (L/m) și b= √ (-L/n) Unde L<0
(Această etapă nu este necesară dacă ecuația este dată în standard de la.

ii. Apoi, înlocuiți partea dreaptă a ecuației cu zero.

iii. Factorizați ecuația și luați soluții

Prin urmare, soluțiile sunt ,

Ecuațiile asimptotelor sunt

Ecuațiile asimptotelor pentru hiperbolarea axei x pot fi obținute prin aceeași procedură.
Găsiți asimptotele unui hiperbolă - Exemplul 1
Luați în considerare hiperbolitatea dată de ecuația x2/ 4-y2/ 9 = 1. Găsiți ecuațiile asimptotelor.

Rescrieți ecuația și urmați procedura de mai sus.
X2/ 4-y2/ 9 = x2/ 22 -y2/ 32 = 1
Prin înlocuirea laturii drepte cu zero, ecuația devine x2/ 22 -y2/ 32 = 0.
Factorizarea și luarea unei soluții a ecuației oferă,
(X / 2-y / 3) (x / 2 + y / 3) = 0
Ecuațiile asimptotelor sunt,
3x-2y = 0 și 3x + 2y = 0
Găsiți asimptotele unui hiperbolă - Exemplul 2
- Ecuația unei parabole este dată ca -4x2 + y² = 4

Această hiperbolă este o hiperbolă a axei x.
Rearanjarea termenilor hiperboliei în standardul oferit
-4x2+ y2= 4 => y2/ 22 -X2/ 12 = 1
Factorizarea ecuației oferă următoarele
(Y / 2-x) (y / 2 + x) = 0
Prin urmare, soluțiile sunt y-2x = 0 și y + 2x = 0.
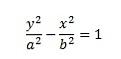 Cum să găsiți asimptotele unui hiperbolă
Cum să găsiți asimptotele unui hiperbolă 